Sorunuzun cevabı HAYIR. Gerilim (veya akım) için böyle bir dalga formu ile reaktans, sinüzoidal sabit durum girişleri ve çıkışları ile kullanılan aynı formülle tanımlanmaz (frekans için faktör 2'de modifikasyon olsun veya olmasın) çünkü reaktans, empedans ve fazör kavramları yalnızca sinüzoidal sabit durum için geçerlidir.

Empedans kavramının uygulanabilirliği

Sinüzoidler, kosinüzoidler ve bunların karmaşık akrabaları olan üsteller, dalga biçimlerini doğrusal zamanla değişmeyen devrelerde muhafaza etme gibi çok özel bir özelliğe sahiptir. Bunun nedeni, üstel fonksiyonun öz benzerliğine indirgeniyor, ancak bir sinüs türevinin kosinüs (başka bir sinüzoidal fonksiyon, yeni kaydırılmış) ve benzer şekilde, daha 'gerçek' bir açıklama düşünebilirsiniz. bir kosinüsün türevi bir sinüstür (tamam, işaret değişikliğiyle, yine de bir faz kayması olarak kaydedilebilir). Ve (doğrusal, zamanla değişmeyen) indüktörlerin ve kapasitörlerin kurucu ilişkisi, türevleri içeren doğrusal ilişkidir. Yani temel olarak: sinüzoidal gerilim veya akım IN ---> sinüzoidal akım veya gerilim OUT.

R, L ve C'li bir devrenin bir sinüzoid üzerinde sahip olabileceği tek etki, onu zayıflatmak ve onu faz kaydırmasıdır. Bu etki, bu iki bilgi parçasını içeren matematiksel bir miktarla tanımlanabilir. Ve tahmin edin, karmaşık bir sayı tam da bunu yapar.

Empedans, bu karmaşık sayı ile tanımlanır. Sinüzoidal bir uyaran ve sinüzoidal tepkiniz var. Fazörler tarafından tanımlandığında, oranları sadece karmaşık bir sayıdır - empedans veya onu nasıl görmek istediğinize bağlı olarak kabul - yanıtın ne kadar zayıflatıldığını ve fazda kaydırıldığını açıklar.

Empedans kavramının uygulanamazlığı

ANCAK tüm bu basitleştirilmiş mekanizma yalnızca sinüzoidal GİRİŞ ve sinüzoidal ÇIKIŞ varsa çalışabilir. Türevler (ve integraller) tarafından "bozulmuş" oldukları için diğer dalga formu şekilleriyle çalışmaz. Bu demektir ki, bir R-L-C doğrusal zamanla değişmeyen devresini sinüzoidal olmayan bir girişle beslediğinizde, empedans kavramı artık kullanılamaz çünkü anlamsız olacaktır.

Devreyi yöneten diferansiyel denklemleri çözerek veya ... sadece bir simülatör kullanarak :-) Tam dalga doğrultulmuş sinüzoidal voltajla bir indüktörü besleyen birkaç LTSpice simülasyonu ve bu voltaj tarafından kontrol edilen akım jeneratörlerini çalıştırdım:

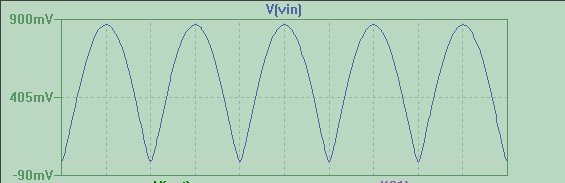
L devresinin doğrultucuyu (yüklediği ve çok fazla) yüklemediğinden emin olmak için voltaj kontrollü voltaj ve akım jeneratörleri kullanmak zorunda kaldım. Sonuçlar çarpıcı şekilde farklı.

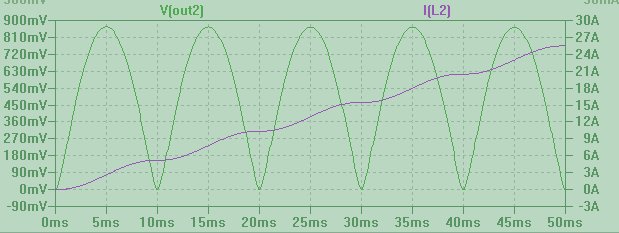
Bu şekle sahip bir voltaj V (çıkış2) bir indüktöre zorlandığında, mor dalga formu I (L2) ile gösterildiği gibi, süresiz olarak oluşan bir akım elde ederiz. Bu şaşırtıcı değil, çünkü akımı elde etmek için gerilimi zamanla entegre etmemiz gerekiyor ve V (çıkış2) asla negatif gitmediğinden, yalnızca ekleyebilir, ekleyebilir ve ekleyebiliriz ...

Ancak bu şekle sahip bir akım I (L1) bir indüktöre zorlanırsa, üzerinden periyodik olarak bozulmuş üçgen benzeri bir voltaj V (çıkış) elde ederiz. Bu çarpıcı şekilde farklı davranışın nedeni, şimdi gerilimin şeklini almak için akımın türevini almamız gerektiğidir.

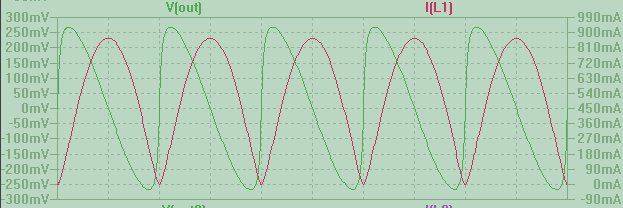
Empedans kavramının, sinyallerin both sinüzoidal ve sabit durum olmasını gerektirdiğini belirtmek gerekir. Yukarıdaki örnek, parçalı bir sinüzoidal uyarıcı kullanmıştır ve her periyotta türev ve integral hala sinüzoidal şekle sahip olmasına rağmen, genel dalga biçimi şekli değildir. Türev dahil olduğunda süreksizliklerimiz var (yukarıdaki simülasyonda, tam dalga doğrultucumda gerçek diyotlar kullandığım için giriş sinyali olduğu için yumuşatıldılar); integral söz konusu olduğunda, sınır koşulları tarafından belirlenen entegrasyon sabitinin değeri nedeniyle bir birikimimiz olur.

Her iki durumda da, üstel, sinüs veya kosinüs olmayan fonksiyonların türevleri ve integralleri genel fonksiyonlarda farklı bir şekilde geri döndüğünden, indüktörün uyarıcı dalga formu üzerindeki etkisini artık basit bir zayıflama ve faz olarak tanımlayamazsınız. vardiya. Sonuç olarak, empedans kavramına veda edebilirsiniz.

Fourier analizi için kurtarma

Yine de, sınırları dahilinde uygularsanız yararlı empedans konseptini kullanabilirsiniz. Sinüzoidal olmayan giriş sinyalini farklı frekanslara sahip sinüzoidlerin toplamına (hatta bir dizi veya periyodik değilse bir integrale) ayırırsanız, her bir sinüzoidal bileşen üzerindeki empedans kavramını kullanarak sinüzoidal bileşenleri bulabilirsiniz. çıkış sinyali ve ardından ortaya çıkan dalga biçimini yeniden yapılandırın.

Elbette, formül hala aynı. Ve evet, temel frekansın orijinal sinüs dalgasından iki katına çıktığı konusunda haklısınız.

Farklı olan, formülün nasıl kullanıldığıdır. Bu reaktans formülü, bir indüktörün zamana bağlı özelliklerinin tek bir frekans temsilidir. Saf bir sinüzoid yalnızca tek bir frekanstan oluşur, böylece bu frekanstaki reaktansı kolayca hesaplayabilirsiniz.

Düzeltilmiş bir sinüzoid, temel frekansın her tam sayı katında sonsuz toplam saf sinüzoidlerden oluşur. Yani, orijinal denklem doğrudur ... ancak bir seferde yalnızca bir frekans bileşeni için. Teknik olarak, (sonsuz) frekans bileşenlerinin her birindeki reaktansı hesaplayarak, ilgilenilen voltajı veya akımı bularak ve sonuçları tüm frekanslar üzerinden toplayarak, ancak devrenizin neye benzediğine ve gerçekte hangi bilgilere bağlı olarak devreyi çözebilirsiniz. sorunu çözmek için farklı bir yaklaşım seçmek isteyebilirsiniz.

Daha fazla bilgi için, rektifiye edilmiş bir sinüzoidin Fourier dönüşümünün ne olduğu dahil, Fourier dönüşümünü araştırmanızı tavsiye ederim.

Vay be!Çektiğiniz giriş voltajı, birkaç terim fourier serisi ile oldukça iyi bir şekilde yaklaşık olarak tahmin edilebilir.

Tepe genliği V olan 50 Hz'lik düzeltilmiş bir sinüs dalgası olan RFCafe'deki bu sayfadan şu bileşenlere sahiptir:

• 0,63 V DC
• 100 Hz, 0,42 V
• 200 Hz, 0,08 V
• 300 Hz, 0,04 V

Bu muhtemelen amaçlarınız için yeterlidir.

Bu kaynağa bağlı bir RL yükünde akan toplam akım şu şekildedir:

Itot = 0.63 * V / R + 0.42 * V / (sqrt (R ^ 2 + (2pi * 100 * L) ^ 2)) + ... vb

Elbette R yokluğunda akım, DC bileşeni nedeniyle sonsuzdur.

Bir şema gösterildikten sonra Chris'in size yapmanızı önerdiği şeyi yapmaya karar verdim. Sayısal olarak simüle edin.

Bu yüzden en sevdiğim simülatör CircuitJS'i seçtim ve sorunuzdaki şemanın aynısını oluşturmaya çalıştım.

Bu benim girişimim:

Simülasyonla etkileşimde bulunabilmeniz için simülasyona bağlantı kurun.

• Yeşil çizgi, indüktör üzerindeki voltajdır
• Sarı çizgi, indüktörden geçen akımdır
• Beyaz çizgi, indüktörün reaktif gücüdür

En soldaki op-amp aşağıdaki matematiksel ifadeye sahiptir \ $ V_ {out} = \ text {abs ($ V_ {in} $)} \ $, giriş 5 V genlikli bir sinüs dalgasıdır. bu voltaj ikinci bir op-amp ile tamponlanır. Her iki op-amp de idealdir, böylece teoride sonsuz akım sağlayabilirler.

O zaman en sağdaki op-amp, ideal bir voltaj kaynağı görevi görür.

Gördüğünüz gibi, indüktörden geçen akım, sonsuzluğa eğilimli olan gerilimin basitçe integralidir. Reaktif güç de aynı şekilde sonsuzluk eğiliminde olacaktır.

Reaktif güç bilindiğinde, reaktans şu şekilde hesaplanabilir:

\ $ Q = \ frac {V ^ 2} {X} \ $

ve biz X istiyoruz

\ $ X = \ frac {V ^ 2} {Q} \ $

Dolayısıyla \ $ V ^ 2 \ $, asla değişmeyecek bir genliğe sahip periyodiktir. Asla daima.

Bu, \ $ X = \ frac {V ^ 2} {Q} \ $ 'nın 0 Ω eğilimi göstereceği anlamına gelir, çünkü görebileceğiniz gibi, Q giderek büyür ve sonsuza doğru büyür (beyaz olarak görülüyor).

Açıkçası orada olması gereken indüktör ile seri olarak basit bir 1 ohm direnç eklemek. Ah! Aptal ben.

Ardından şuna benzer bir şey elde edersiniz:

Bununla etkileşimde bulunmak istiyorsanız, işte bu şemaya bağlantı.

Grafikler yukarıdakilerle aynıdır.

Derp, bu soruyu doğru bir şekilde düzenlemek için çok yorgun. İsteyen varsa düzenleyin. Değilse, yapma. Adjö çocuklar.

Hayır, çünkü bu formül (\ $ X = 2 \ pi f L \ $) sinüs dalgalarının özelliklerine dayanır ve düzeltilmiş AC sinüs dalgası değildir.

Endüktansın tanımı, L:

$$ V = L \ frac {dI} {dt} $$

Burada indüktörden geçen akım ve V, bunun üzerinden indüklenen voltajdır (zamanın I ve V fonksiyonlarıyla, t).

Akım sinüzoidal ise, $$ I = \ sin (2 \ pi f t) $$ f frekansı ile.Farklılaştırma şunu verir: $$ V = 2 \ pi f L \ cos (2 \ pi f t) $$

Öyleyse voltaj dalga biçimi de sinüzoidaldir, ancak 90 derecelik bir faz kayması (sin'den cos'a) ve \ $ 2 \ pi f L \ $ çarpım faktörüne sahiptir, ki bu belirttiğiniz reaktansın büyüklüğüdür.

V ve / veya ben sinüs dalgası değilsem, bu ilişki geçerli değildir.